6enmate :D: 0.999... = 1 ¿Quééééééé?

miércoles, 3 de noviembre de 2010

0.999... = 1 ¿Quééééééé?

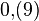El número 0,999... que también se puede escribir como $\textstyle 0,\!\bar{9}$ ó $\textstyle 0,\!\dot{9}$ ó $\textstyle 0,\!(9)\,\!$ denota un número real igual a 1. Es decir, las notaciones "0,999..." y "1" representan el mismo número real. Aunque aparentemente contradictoria, esta igualdad es válida y se pueden proporcionar demostraciones con diferentes grados de rigor y tiene su origen en que la representación decimal de un número real no es necesariamente única.

Las diferentes demostraciones son las siguientes:

Algebraica (en su forma simplificada):

$1 = \frac{9}{9} = 9 \times \frac{1}{9} = 9 \times 0,111\dots = 0,999\dots$

Con manipulación de dígitos:

$\begin{align} x &= 0,999\ldots \\ 10 x &= 9,999\ldots \\ 10 x - x &= 9,999\ldots - 0,999\ldots \\ 9 x &= 9 \\ x &= 1 \\ 0,999\ldots &= 1 \end{align}$

Analítica:

$0,999\ldots = \lim_{n\to\infty}0,\underbrace{ 99\ldots9 }_{n} = \lim_{n\to\infty}\sum_{k = 1}^n\frac{9}{10^k} = \lim_{n\to\infty}\left(1-\frac{1}{10^n}\right) = 1-\lim_{n\to\infty}\frac{1}{10^n} = 1.\,$

Publicado por: Alberto Valdivia

1 comentario:

Unknown3 de noviembre de 2010, 19:20
Muy interesante tu publicacion yo solo pense q se redondeaba nomas y daba el 1 pero ahora veo q hay mas formas muy bueno :)

Por:Juan Diego Urbano 4to C
ResponderEliminar
Respuestas