Paradoja del cuadrado perdido

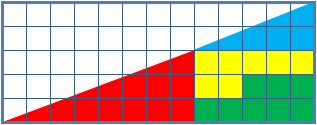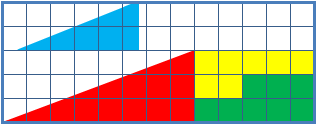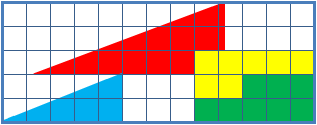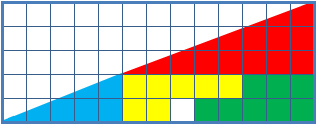
La paradoja del cuadrado perdido es una ilusión óptica usada en clases de matemáticas, para ayudar a los estudiantes a razonar sobre las figuras geométricas. Está compuesta de dos figuras en forma de triángulo de base 13 y altura 5, formadas por las mismas piezas, donde uno aparenta tener un "agujero" de 1×1 en él.
La clave de la paradoja está en el hecho de que ninguno de los triángulos tiene la misma área que sus piezas componentes. El área de cada pieza es:
Pieza roja: 12 cuadrados.
Pieza verde: 8 cuadrados.
Pieza amarilla: 7 cuadrados.
Pieza azul: 5 cuadrados.
Las cuatro figuras (amarilla, roja, azul y verde) ocupan un total de 32 cuadrados, pero el triángulo tiene 13 de base por 5 de altura, lo que supone un área de 32,5 cuadrados.
La paradoja tiene una explicación simple: la figura presentada como un triángulo no lo es en realidad, debido a que en realidad tiene cuatro lados, y no los tres propios del triángulo. La "hipotenusa" no está formada por una recta, sino por dos con pendientes ligeramente distintas. Si comparamos los ángulos de inclinación de la hipotenusa respecto de la base de los triángulos rojo y azul vemos que son distintos. En el triángulo rojo el ángulo es 20.55°, mientras que en el azul es 21.8°. Así, la suma de los tres ángulos en la figura de arriba es menor que 180°, mientras que en la figura de abajo la suma de los tres ángulos es mayor que 180°.

Publicado por: Alberto Valdivia