Cono
| 1 | INTRODUCCIÓN |
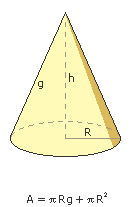
Área total de un cono recto, donde g es la generatriz y R el radio de la base.
Cono (geometría), o cono circular recto, es el cuerpo de revolución engendrado por un triángulo rectángulo al girar alrededor de uno de sus catetos.
La hipotenusa del triángulo es la generatriz, g, del cono. El cateto sobre el cual se gira es la altura, h. El otro cateto es el radio, r, de la base.
El desarrollo de la superficie de un cono en el plano da lugar a un sector circular de radio g y ángulo (r/g)·360º:
| |
La superficie lateral de un cono recto es prg. Por tanto, su superficie total es: Atotal = prg + pr2
El volumen de un cono recto es:
| |
| 2 | TRONCO DE CONO |
Área total de un tronco de cono recto de bases paralelas, donde g es la generatriz y r y R los radios de las bases.
Un tronco de cono recto de bases paralelas es la porción de cono comprendido entre la base y una sección paralela a ella. Es el cuerpo de revolución generado por un trapecio rectángulo al girar alrededor del lado perpendicular a las bases.
| |
Queda caracterizado por los radios de las bases, r y r’, la altura, h, y la generatriz, g, entre las cuales se da la siguiente relación: g2 = (r – r’)2 + h2
El área lateral de un tronco de cono es: Alat = p·(r + r’)·g
Su volumen es: V = p·(r2 + r’2 + rr’) ·h/3
| 3 | CONO OBLICUO |
Un cono oblicuo es el cuerpo geométrico resultante de cortar un cono recto mediante un plano oblicuo a su eje y que corte a todas sus generatrices.
Allison Regalado Sosa N° 26 4B♥
| |







No hay comentarios:
Publicar un comentario